In this article, we will explore a critical aspect of optical design: the K correlation, and how it plays a pivotal role in managing issues such as stray light and light scattering in optical systems, and we will discuss the Bidirectional Scattering Distribution Function (BSDF) in greater detail.
The Significance of K Correlation
In optical design, K-correlation is typically used in the context of the Bidirectional Scattering Distribution Function (BSDF). The BSDF describes how a surface scatters light in various directions. The K-correlation factor provides a quantitative link between the BSDF of a surface and the surface roughness or irregularities.
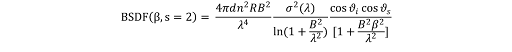
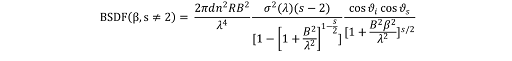
where s is the effective RMS surface roughness, s is the log-log slope of the BSDF at large spatial frequencies, and β is defined as the sine of the scatter angle (ϑs) minus the sine of the specular reflection/transmission angle.
The K-correlation factor can be expressed using the following equation:
K = BSDF/A
Where A is the incident radiant flux on the surface, which depends on the angle of incidence.
The K-correlation factor is a dimensionless quantity that helps optical designers understand how surface imperfections affect the scattering of light. It essentially normalizes the BSDF by the incident radiant flux, making it a valuable tool for quantifying light scattering in optical systems.
By using the K-correlation factor, optical experts can assess the impact of surface roughness and imperfections on the performance of optical components. This information is crucial for making informed decisions about materials, coatings, and design modifications to reduce stray light and light scattering, ultimately leading to the optimization of optical systems.
Controlling Stray Light
Stray light is a common problem in optical systems that can lead to reduced image quality and performance. It occurs when unwanted light enters the optical path, often due to surface imperfections or unintended reflections. K correlation helps us assess the extent of stray light and, more importantly, enables us to take steps to mitigate it.
With K correlation analysis, optical designers can identify areas where stray light might be problematic. This includes understanding how various optical components scatter and reflect light and, therefore, how stray light is generated. With this information, designers can make informed decisions about coatings, baffles, and optical layout to minimize stray light.
Managing Light Scattering
Light scattering is another critical aspect of optical design that K correlation addresses. When light interacts with surface irregularities or contaminants, it can scatter in various directions, leading to reduced image contrast and quality. By quantifying light scattering, K correlation helps designers optimize optical systems to minimize this effect.
Optical engineers use K correlation to simulate and predict how light will scatter within an optical system. This insight is invaluable when designing lenses, mirrors, and other optical components. By analyzing the scattering behavior of these components, designers can make informed choices about materials and surface quality to reduce light scattering, ensuring the final optical system performs optimally.
The Role of the Bidirectional Scattering Distribution Function (BSDF)
The Bidirectional Scattering Distribution Function (BSDF) is a critical tool in understanding how surfaces scatter and reflect light. It provides a comprehensive description of the scattering behavior of surfaces, which is fundamental to K correlation analysis.
The BSDF essentially quantifies how much light is scattered in different directions when it interacts with a surface. By integrating the BSDF data into K correlation calculations, optical designers gain a detailed understanding of how surface imperfections contribute to stray light and light scattering.
The BSDF also plays a crucial role in predicting and managing light scattering. It provides a detailed map of how light interacts with a surface, allowing designers to identify which areas are more prone to scattering. Armed with this information, they can make design adjustments to minimize light scattering and improve optical performance.
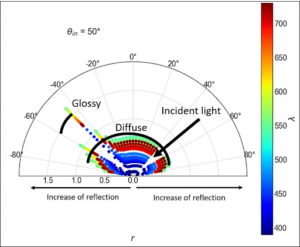
Figure 1. The measurement of the BSDF shown for each wavelength. Image from Eclat-Digital
The Practical Application of K Correlation and the BSDF
Understanding the theory behind K correlation and the BSDF is essential, but how are these concepts applied in real-world optical design?
1. Design Optimization
K correlation and the BSDF guide optical designers in selecting the most appropriate materials and surface finishes to minimize stray light and light scattering. This optimization process ensures that optical systems deliver the highest image quality and efficiency.
2. Stray Light Analysis
Through K correlation, designers can perform in-depth stray light analysis. This involves simulating various scenarios to identify potential stray light sources and take measures to prevent their impact on the final image.
3. Coating Selection
Coatings are essential to control reflections and minimize stray light. K correlation assists in selecting the right coatings to achieve the desired optical performance.
4. Realistic Simulations
K correlation and the BSDF enable optical designers to create realistic simulations of how light interacts with various surfaces. This level of simulation precision helps in fine-tuning optical systems.
Conclusion
In optical design, managing stray light and light scattering is of great importance. K correlation, with the support of tools like the Bidirectional Scattering Distribution Function (BSDF), empowers optical designers to tackle these challenges head-on. By understanding how surface imperfections affect light distribution, they can make informed decisions that result in superior optical systems.
For more in-depth information on the Bidirectional Scattering Distribution Function (BSDF), please refer to the article Bidirectional Scattering Distribution Function in our OFH website