An optical system is only as strong as its weakest link. When designing an imaging system, sensor resolution is just one important factor and it is important to ensure sensors and detectors are well matched.
Take these scenarios:
- Taking a selfie with your cockadoodle
- Placing a digital sensor on top of your microscope
- Photo shooting your fig cronut with your new digital camera
In the simplest terms, the above are all composed of an object, an imaging object or lens, and a sensor composed of a collection of tiny light-buckets called pixels. Pixels detect light by converting photons into electricity.

Light traveling from an object is modulated by an objective forming an image on the detector
Need assistance designing a custom optic or imaging lens ? Learn more about our design services here.
How do you figure out how many pixels do you need? Well, this depends on lens aberrations, diffraction, and trade-offs between the aperture size and focus.
Aberrations
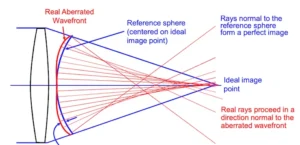
Aberrations are image imperfections and are either chromatic or monochromatic. Chromatic aberrations are related to color: only certain colors are focused well or colors break up and reach different detector areas transforming a white line into a rainbow stripe. Monochromatic aberrations are due to inappropriate design and lens placements. These come in many flavors including spherical, astigmatism, coma, and distortion, as well as subtypes within each.
Diffraction
To ensure sharp images, lens designers need to consider existing lens limiting factors such as diffraction. Diffraction is a concern with light passing an edge such as the lens circumference and such a lens would be labeled diffraction limited.
The impact of diffraction on picture quality is expressed by the f-number, written as f/#. Note this is ratio-not a quotient-of the lens’ focal length to the diameter of its entrance pupil.
f/#=(focal length) ÷ (pupil diameter)
For an ordinary lens, the diameter is the lens diameter. In the presence of an iris, the diameter is usually the diameter of the iris.
EXAMPLE 1, no iris
- Lens: 500 mm focal length, 100 mm diameter
- f/#=(500 mm) / (100 mm) = 5
- The f/# is f/5, pronounced “the eff-number is eff-five”
EXAMPLE 2, with iris
- Lens: 500 mm focal length, 100 mm diameter
- Iris: 50 mm diameter
- f/#=(500 mm) / (50 mm) = 10
- The f/# is f/10
By reducing a camera lens from f/5 to f/10, the depth of focus increases and the image becomes dimmer. By linking f-number to diffraction, this would inform how far apart two things must be for the detector to distinguish them. Thanks to Lord Rayleigh, this figures in the formula:

Here, x is the minimum distance between distinct points in the image, and λ is the wavelength. Thus, the shorter the wavelength (purple light being the shortest), the more pixels are needed.
Say you are taking a photograph of two purple Christmas tree lights from far away. At f/8, and purple light, x = 3.7 microns, meaning their images must be > 3.7 microns apart for their image to change from one bump to two.
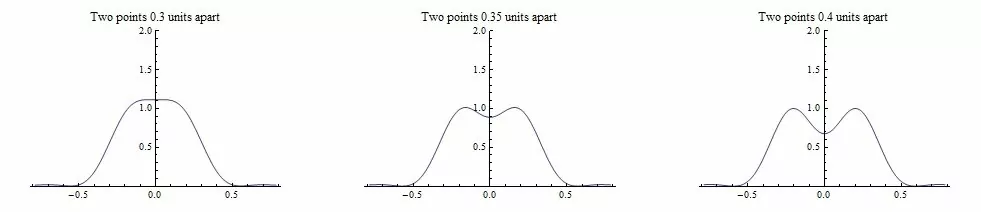
As objects are moved farther apart, their images become more discernable
While lower f-numbers are better for resolving fine image details, the lens center works better than its periphery. To minimize diffraction while maximizing the useful lens area, you might choose in photography an f-stop in the middle of the available range, say f/8.
In general, larger diameter lenses collect more light. For tiny lenses such as those in cell phone cameras, exposure times are lengthened to ensure images are not dim.
To illustrate, let’s look at design considerations in the following scenarios.
A POINT AND SHOOT CAMERA
In a camera, a lens system produces a focused image of an object onto a detector. Assuming an f/8 camera lens, you’re wasting detector-pixels if you are examining details closer than 3.7 microns at the detector.
In practice, we try to fit at least two pixels across each minimum feature size and we therefore, in monochrome, care about 2×2 pixel clumps. According to the Nyquist Sampling theorem, you need to “sample” a signal at least twice as often as the fastest changing part you wish to examine. There is an additional factor relevant to color photography but to keep things simple, we will limit this to monochromatic imaging.
Building on the purple light example, we will use 1.8 micron pixels. A common-sized “1/3” digital camera sensor measures 4.8 mm x 3.6 mm. In this case, the narrow axis of the sensor ought to have fewer than:
((3.6 mm)(1000 microns/mm) / (1.8 microns per pixel as above)) = 2,000 pixels
Efficient resolution=2,667 x 2,000 pixels=5.3 megapixels
If the vendor had packed, say, 10 megapixels into the area of a “1/3” digital sensor in an f/8 monochrome system, it’s probably not worth paying for that. On the other hand, if a sensor of that size only has 200,000 pixels, you might be missing a lot of detail.
A MACHINE VISION SYSTEM
The number of pixels needed here depends on the size of the imaged object and the detail required.
Suppose the object is a 27” square containing typewritten text and symbols composed of fine straight lines, like a UPC barcode. To figure out how many pixels the sensor needs:
What are we looking at?
- Our square object measures 686 x 686 mm
- The finest detail desired is 0.5 mm, the width of a single printed line
- The finest picture detail should be projected on 2 or more pixels per axis.
- We have a decent-quality, affordable lens able to resolve a certain number of “line pairs/mm”, say 40 line-pairs/millimeter, or 80 dots/mm, or 2,032 dots/in
Design plan
- We need to resolve 1,372 dots along each side of the object (686/ 0.5)
- To project each dot onto two sensor pixels in each direction, we need at least 2,744 pixels along each side of the sensor
- Fora sensor with a 4:3 imaging ratio, we need at least 10 megapixels: 2,744 × 3,659.
In summary, when designing a camera system, you need to consider:
- The impact of f/# on resolution, cost, diffraction effects, and depth-of-focus
- The effect of lens size and its useful area on focus and brightness
- The value an experienced optical engineer brings in accurately predicting resolution of an optical system
The authors thank Matthias Ferber for useful discussion about this article.