As mentioned in several articles in this blog, aberrations are of great relevance when designing an optical system. The objective being to design a system that creates a “good image”. However, there are different metrics to evaluate what is a “good image”. Most of the time, a customer won’t express their image quality requirements in terms such as MTF or ray aberration plots. However, they know what they want the optical system to do. It is up to the optical engineer to translate those needs into a numerical specification. Some aberration measurement techniques are better for some applications than for others. For example, for long-range targets where the object is essentially a point source like in a telescope, RMS wavefront error might be an appropriate choice for system evaluation.
RMS wavefront error is a way to measure wavefront aberration. Basically, we compare the real wavefront with a perfect spherical wavefront. We are not going to derive the equation to physically calculate the RMS wavefront error. Here we will just say that the RMS wavefront error is given by a square root of the difference between the average of squared wavefront deviations minus the square of average wavefront deviation. The RMS value expresses statistical deviation from the perfect reference sphere, averaged over the entire wavefront.
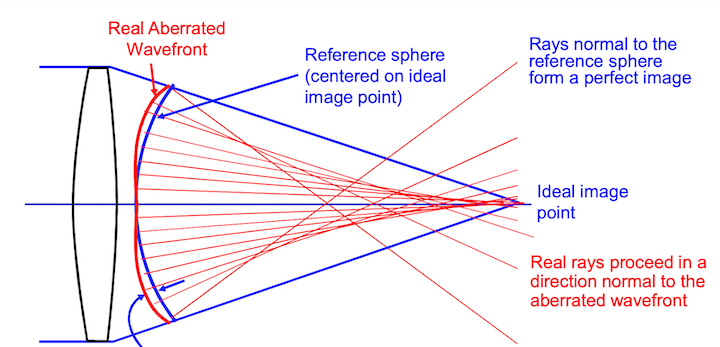
When calculating the wavefront error, the reference sphere is centered on the “expected” image location (usually the image surface location of the chief ray). It may be that a different reference sphere will fit the actual wavefront better. If the center of the better reference sphere is at a different axial location than the expected image location, there is a “focus error” in the wavefront. If the center of the better reference sphere is at a different lateral location than the expected image location, there is a “tilt error” in the wavefront
RMS Wavefront Error in Zemax
Ray trace programs will report “Wavefront Errors” at the Exit Pupil of a system. The errors are the difference between the actual wavefront and the ideal spherical wavefront converging on the image point. In a system with aberrations, rays from different positions in the exit pupil may miss the ideal image position by various amounts when they reach the image plane. This is known as “Transverse Ray Aberration”, or ‘TRA’.
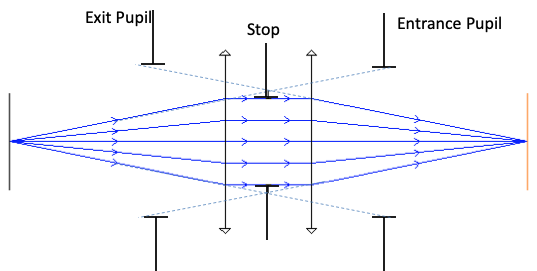
Zemax does not normally propagate waves through an optical system but rather uses a geometric relationship between Ray errors and wavefront errors to calculate the wavefront error map. Since rays are always perpendicular to wavefronts, a wavefront tilt error (at some location in the pupil) corresponds directly to a Transverse Ray error (TRA) at the image plane. By tracing a number of rays through the pupil,and measuring the TRA of each, we can get the slope of σ; then by numerical integration, we can find the wavefront aberrations, σ.
Measuring Wavefront errors in real systems
There are different ways to measure the wavefront distortions introduced by an optical system. We can use interferometric methods, however these may be limited to the use of coherent light (like a laser). Shack-Hartmann wavefront sensors can work in incoherent and even broad-band light. A Shack-Hartmann wavefront sensor consists of an array of micro-lenses focusing portions of an incoming wavefront onto position-sensitive detectors.
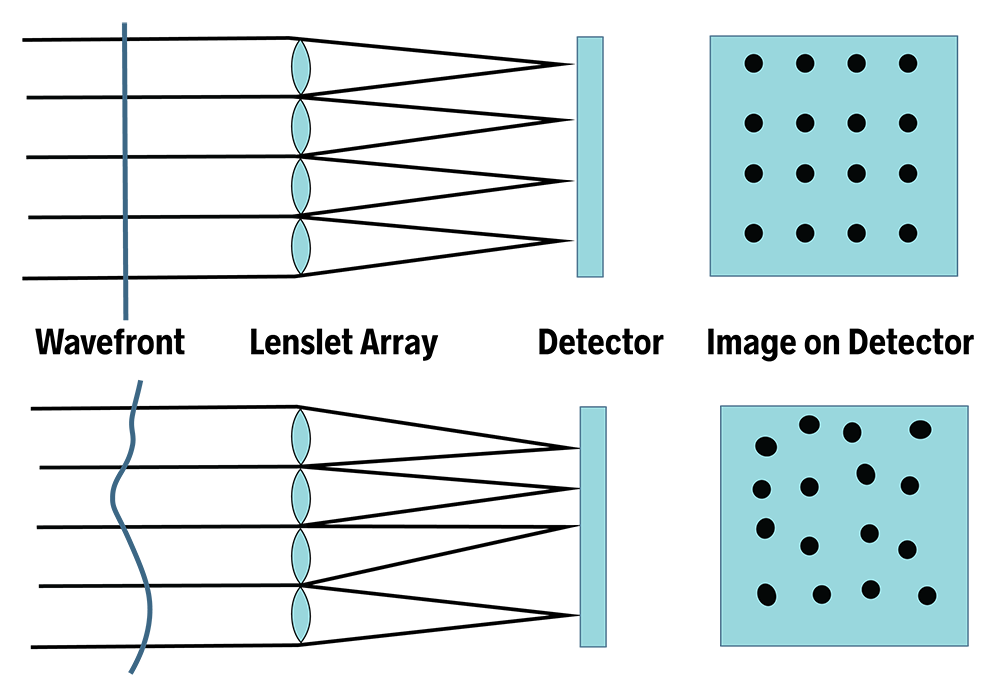
example of wavefront error
Shack–Hartmann sensors are used in astronomy to measure telescopes and in medicine to characterize eyes for corneal treatment of complex refractive errors
