Understanding Strehl Ratio: A Practical Overview
The Strehl ratio stands as a fundamental metric in optical engineering, providing a concise measure of the quality of an optical system in comparison to an ideal, aberration-free counterpart. This practical overview aims to shed light on the significance and computation of the Strehl ratio, offering insights into its role in assessing optical system performance.
Defining the Strehl Ratio:
At its core, the Strehl ratio quantifies the degradation of optical system performance caused by aberrations. It achieves this by comparing the intensity of the central maximum in the Point Spread Function (PSF) of the real optical system to that of an idealized aberration-free system. Expressed as a ratio, a Strehl ratio of 1 indicates a perfect optical system, while values below 1 signify the presence of aberrations and a reduction in optical quality.
Incorporating the Point Spread Function:
The PSF is a crucial element in understanding the Strehl ratio. It represents the intensity distribution of the light emerging from an optical system, forming an image of a point source. The Strehl ratio takes into account the central maximum of this PSF, comparing the peak intensity of the actual optical system to the theoretical peak intensity of an aberration-free system.
Calculation and Interpretation:
The Strehl ratio is mathematically calculated as the ratio of the maximum intensity of the PSF of the real optical system (I_real) to the maximum intensity of the PSF of an aberration-free system (I_ideal). The formula is expressed as Strehl Ratio = I_real / I_ideal.. Interpreting the Strehl ratio involves understanding how close the real optical system is to the theoretical ideal. A Strehl ratio of 1 indicates minimal aberrations and excellent optical performance, while lower values suggest the presence of aberrations and a decrease in image quality. The diffraction pattern of a rotational symmetry optical system has an axial symmetrical pattern. The pattern cross section has a central maximum where 83.9 % of total energy is encircled. The radius of the central disc is called “Airy disc” and is defined by
R(airy) =1.22 λ f/#w where λ is working wavelength, f/#w is working F-number.
Need assistance designing a custom optic or imaging lens ? Learn more about our design services here.
When designing an optical system, the Strehl ratio is used to estimate the required correction of wavefront aberrations.
The acceptable level of wavefront aberrations is different for every application but a value of 0.80 Strehl is conventionally used to define an optical system as “Diffraction limited” or ideal.

Aberration-free Fraunhofer diffraction pattern 3-D shape

Fraunhofer diffraction patterns 2-D intensity map at the image plane.
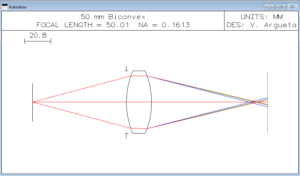
Below are Zemax PSF plots based on real optical system designs
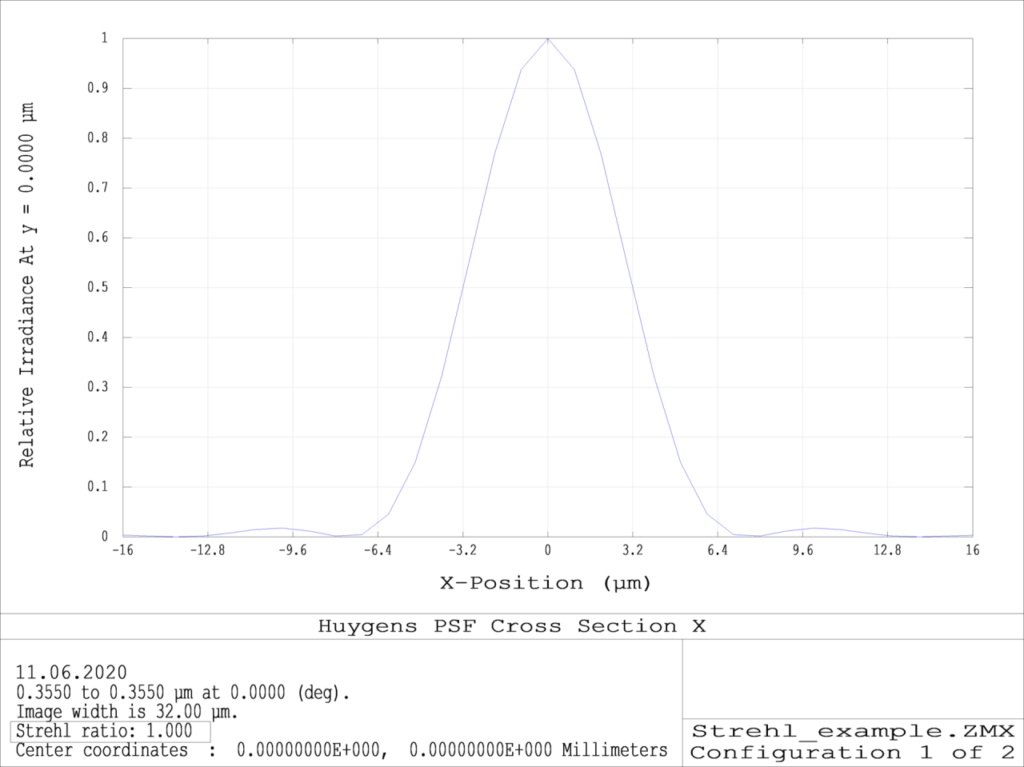
PSF cross section
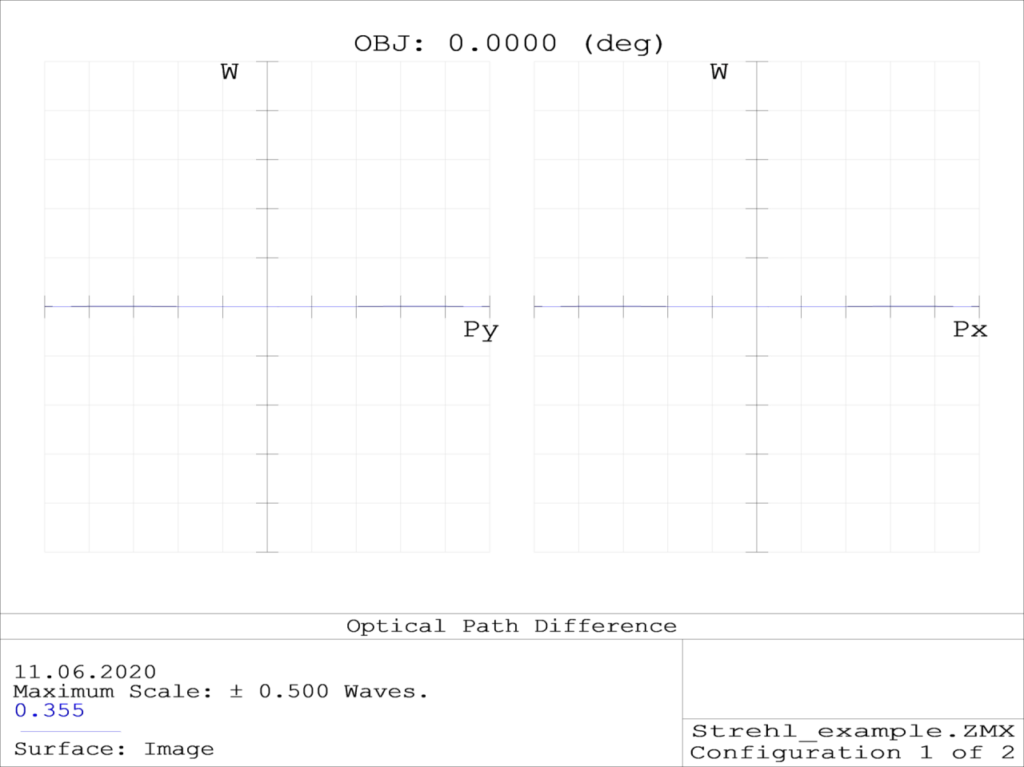
Optical path difference
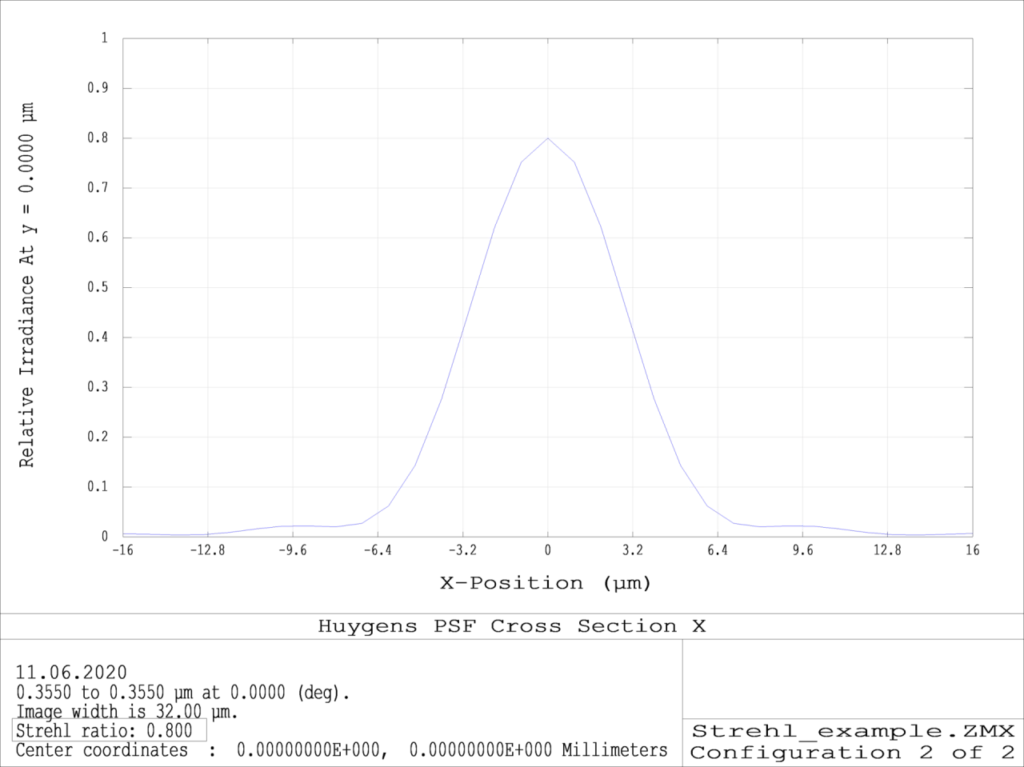
PSF cross section
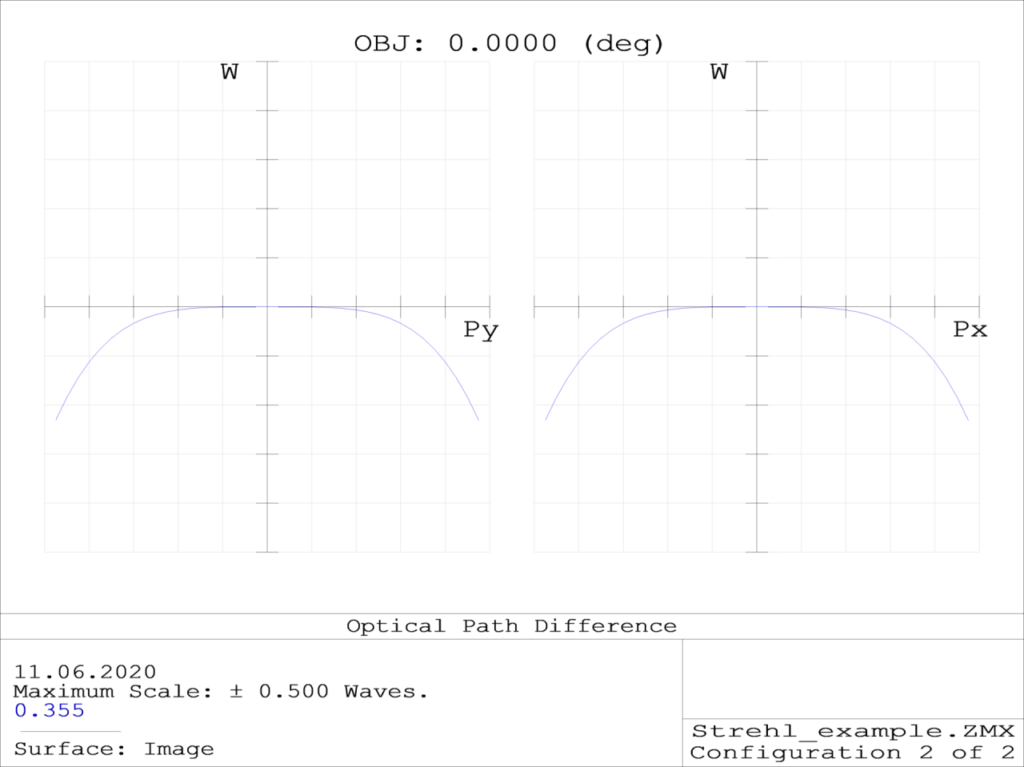
Optical path difference
In the above system, wavefront aberrations correspond to 0.25 λ Peak-to Value-this matches to Rayleigh ¼-wave PV criteria of image quality provided by a “Diffraction limited” system.
MTF plot corresponding to 0.8 Strehl ratio is shown in the final image
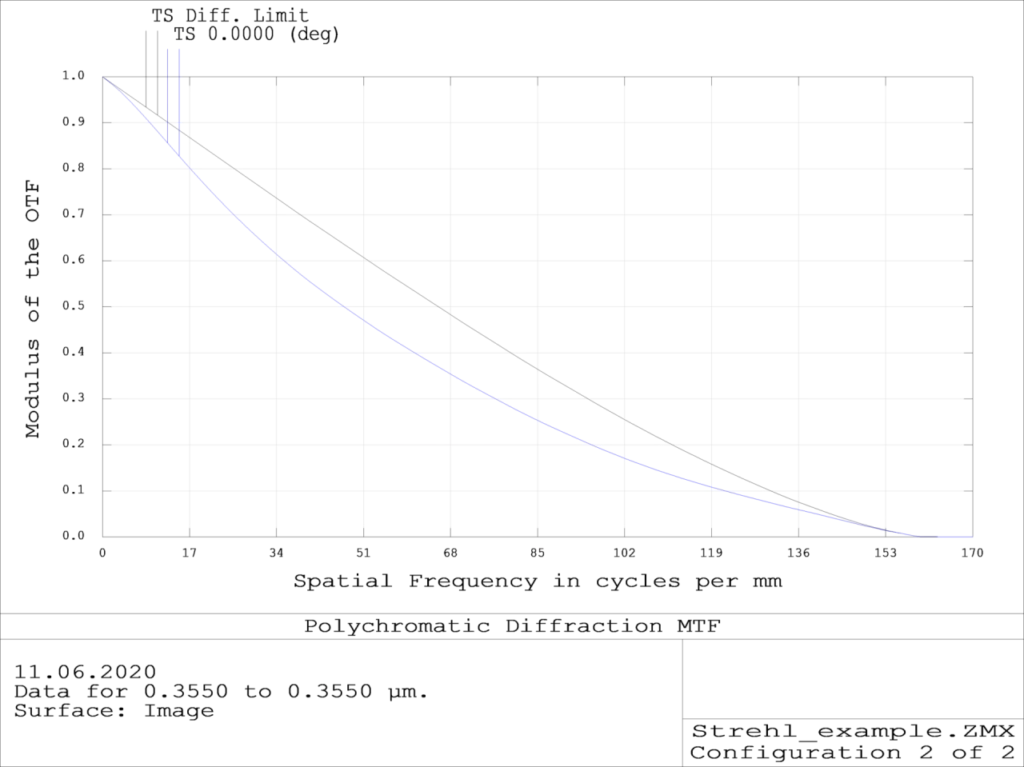
Insights into Wavefront Error and Its Impact
Understanding wavefront error is pivotal in the realm of optics, providing profound insights into the performance and limitations of optical systems. Here are key insights into wavefront error and its impact:
- Aberrations as Distortions: Wavefront error primarily manifests as aberrations, introducing distortions in the way light propagates through an optical system. These distortions can take various forms, such as blurring, asymmetry, or color fringing, and are critical factors in determining the optical quality of an imaging system.
- Impact on Imaging Quality: The level of wavefront error directly correlates with the imaging quality of optical systems. Higher wavefront error values result in reduced image sharpness, clarity, and resolution. In applications like photography, microscopy, and astronomy, minimizing wavefront error is essential for capturing detailed and accurate images.
- Challenges in Precision Instruments: Precision optical instruments, including telescopes, microscopes, and cameras, face significant challenges when dealing with wavefront error. Achieving high precision requires meticulous correction of aberrations to ensure optimal imaging performance, especially in applications where the tiniest details matter.
- Applications in Corrective Optics: Understanding wavefront error is a driving force in the development of corrective optics. Techniques such as adaptive optics and specialized lens designs aim to counteract the impact of aberrations, enabling optical systems to deliver improved performance even in challenging environments, such as turbulent atmospheres in astronomy.
- Role in Laser Systems: Wavefront error is particularly crucial in laser systems, where precise focusing and collimation are essential. High-quality laser beams with minimal wavefront error are critical for applications like laser material processing, medical laser procedures, and free-space optical communication, ensuring accuracy and efficiency in these processes.
- Quantitative Assessment with RMS Wavefront Error: The Root Mean Square (RMS) wavefront error provides a standardized and quantitative measure of the overall aberrations present in an optical system. Engineers and designers use RMS wavefront error to numerically assess and compare the optical quality of different systems, guiding efforts to minimize aberrations during the design and manufacturing processes.
- Advancements in Measurement Techniques: The ability to measure wavefront error accurately has seen significant advancements with the advent of technologies such as Shack-Hartmann wavefront sensors and interferometry. These techniques allow for precise characterization of aberrations, facilitating targeted corrections and optimization of optical systems.
- Multidisciplinary Impact: The impact of wavefront error extends across various disciplines, from astronomy and medical imaging to industrial applications and consumer electronics. As technologies advance and the demand for higher precision grows, the understanding and management of wavefront error become increasingly crucial for innovation and progress in diverse fields.
Real-World Applications: Strehl Ratio and Wavefront Error in Action
The practical significance of the Strehl ratio and wavefront error extends across various real-world applications, shaping the landscape of optical design and performance in tangible ways.
- Astronomy – Adaptive Optics Systems: In astronomy, where clarity and precision are paramount, the Strehl ratio and wavefront error play a crucial role. Adaptive optics systems utilize these metrics to assess and correct for atmospheric distortions in real-time. By continuously monitoring and adjusting the optical system based on wavefront error measurements, telescopes can achieve higher Strehl ratios, resulting in sharper and more detailed astronomical observations.
- Medical Imaging – Laser Eye Surgery: In the realm of medical imaging and ophthalmology, the Strehl ratio and wavefront error are pivotal in the success of laser eye surgeries, such as LASIK. These procedures involve reshaping the cornea to correct refractive errors. Precise measurements of wavefront error guide the laser in sculpting the cornea to achieve optimal vision correction. The Strehl ratio serves as a quantitative indicator of the surgical outcome, ensuring improved postoperative visual quality.
- Microscopy – Super-Resolution Imaging: In advanced microscopy techniques like super-resolution imaging, the Strehl ratio and wavefront error are critical for pushing the boundaries of optical resolution. By minimizing aberrations through accurate wavefront error measurements, super-resolution microscopes can achieve higher Strehl ratios, enabling researchers to visualize cellular structures at unprecedented levels of detail and clarity.
- Communication – Free-Space Optical Communication: Free-space optical communication systems, which transmit data using laser beams through the atmosphere, benefit from Strehl ratio and wavefront error considerations. By optimizing optical systems to minimize aberrations, these communication systems can achieve higher Strehl ratios, leading to improved signal quality and reliability over long distances.
- Lithography – Semiconductor Manufacturing: In semiconductor manufacturing, precise optics are essential for lithography processes. Controlling wavefront error ensures accurate patterning of circuits on semiconductor wafers. The Strehl ratio becomes a valuable metric in evaluating the performance of optical systems used in lithography tools, contributing to the production of high-quality integrated circuits.
- Space Exploration – Remote Sensing Instruments: Instruments used in space exploration, such as remote sensing devices on satellites, heavily rely on accurate wavefront error measurements and Strehl ratio assessments. These metrics ensure the optimal performance of optical systems, enhancing the quality of images captured from space and providing valuable data for scientific research and Earth observation.
In these diverse applications, the Strehl ratio and wavefront error measurements are not merely theoretical concepts but practical tools guiding the design and operation of optical systems. Their implementation contributes to advancements in fields ranging from astronomy and medicine to manufacturing and space exploration, demonstrating the indispensable role of precise optical performance metrics in shaping our technological landscape.
Conclusions
In conclusion, optical system designers are presented with several key takeaways as they navigate the intricate realm of wavefront error and its impact. It is imperative for designers to recognize the direct link between wavefront error and optical quality, emphasizing the importance of minimizing aberrations to ensure clear, sharp, and high-resolution images. The pursuit of precision stands as a central tenet across diverse applications, spanning telescopes for astronomy, microscopes for biology, and laser systems for manufacturing. The integration of adaptive optics and corrective measures becomes vital, empowering optical systems to dynamically adapt to changing conditions and correct aberrations in real time.
Quantitative assessment through metrics like Strehl Ratio wavefront error provides designers with a systematic approach to compare different configurations, make informed decisions during the design phase, and prioritize corrective actions. Acknowledging the interdisciplinary nature of the field, collaboration with experts in materials science, computer science, and metrology is key to leveraging advancements in materials, computational methods, and measurement techniques.