Introduction
The refractive index is one of the basic concepts in optical sciences. Same as volume, and density, the refractive index is a fundamental property of all materials. However, not only materials that are used in optics have a refractive index. For example, the refractive index of water is 1.33, and the refractive index of air is around to 1.0.
In today’s article we will talk a little bit in depth about the refractive index. This article is a little bit heavy on the math, but if you want to read the short version we have prepare a small summary right here:
Five Essential Things to Learn About the Refractive Index
The Refractive index is a positive dimensionless number bigger than 1.0
It can help you calculate the speed of light when it travels inside a material
The refractive index of a material changes with temperature
A material will have different values of refractive index for different colors.
Scientist have been able to create materials with negative refractive index.
Refractive Index Review
The basic definition of refractive index is that it is an dimensionless number that relates the speed of light in a medium versus the speed of light in a vacuum. In general, it can be expressed by the following equation:
![]()
where n is the refractive index, v is the speed of light in a material, and c is the speed of light in a vacuum. Some important properties can be derived from this simple formula.
1.-Since we cannot exceed the speed of light in a vacuum, n will always be larger than 1
2.- The refractive index will always be positive
Wavelength Dependence
This equation is not complete however. We know, for example, that each wavelength experiences a different refractive index but we don’t see that wavelength dependence in the equation above. It is therefore necessary to expand our simple formula to account for these changes. This is the purpose of Cauchy’s equation
![]()
where n is the refractive index, l is the wavelength of light in vacuum, and A, B, and C are coefficients obtained by direct measurement. Couchy’s equation is usually reduced to the first two terms, so you only need to calculate the A and B coefficients. Although Caucy’s equation is more accurate than the original, it is only valid in the visible range and only for materials with low dispersion. An improvement over this equation can be found in the Sellmeier Equation:
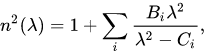
One important difference in this equation is that the denominator in the summation represents absorption lines at specific wavelengths. When working at wavelengths far away from these absorptions lines (thats l >> C), the Sellmeier equation is simplified to:
![]()
This brings us to another important property of the refractive index and that is its relationship with the electrical permittivity and magnetic permeability.
Maxwell’s Equations
Using Maxwell’s equations, we can derive and express for the velocity of an electromagnetic wave in a medium that leads to the expression:
![]()
where ?r is the electric permittivity and ?r is the magnetic permeability (usually with a value of 1 for non-magnetic materials at optical wavelengths). In absorbing materials, it is possible to have a complex electric permittivity leading to a complex refractive index
![]()
where κ is the extinction coefficient
Negative Refractive Index
In nature, we have only found materials with positive refractive indices but it is possible to create materials with negative ones. These materials are called metamaterials and are the 1967 brainchild of Victor Vesalago from the Moscow Institute of Physics and Technology. He predicted that, if a material had a negative electric permittivity and a negative magnetic permeability, it would present a negative refractive index. It would take more than 30 years before his predictions were confirmed in 2000 by Dr. David R. Smith’s from UCSD. His research team produced a new class of materials that exhibited unusual physical properties that had never been observed in nature. These materials obey the laws of physics but behave differently from normal materials (e.g. inverting Snell’s law).

Material with negative refractive index
When it comes to the design of illumination or imagining lenses, we have a vast glass catalogue that we can select from. Choosing the right material can be a daunting task and there is no standard procedure.
Selecting the right glass or plastics material will depend on several factors like operational wavelengths, range of temperature at which the system will operate, presence of abrasive materials, mechanical stress, materials costs, glass melt frequency, and more. Picking the right lens is part art part science and it highly depends on the experience of the optical engineer doing the design. Glass catalogues from companies like Schott usually include several parameters besides refractive index that can help an optical engineer pick the right material. Once the right lens material is selected, we need to specify the refractive index tolerance in the lens schematic as shown in the bottom of this lens manufacturing drawing explanation guide.