Introduction
When working with lasers it is important to understand the physical parameters that define system performance. While some of these specifications may be readily recognizable, such as wavelength and divergence, others may be lesser-known, yet equally critical metrics. For instance, concepts like the M-factor, beam caustic, and Rayleigh Range often have immense significance in shaping the behavior and efficacy of laser systems. Working with these parameters requires a deeper understanding of the interplay between light, optics, and the underlying physics governing laser technology.
Basic Principles of Rayleigh Range
Named after the eminent British physicist Lord Rayleigh, the Rayleigh Range delineates the distance over which a laser beam’s intensity remains relatively stable before significant divergence takes place. At its core, the Rayleigh Range is a manifestation of diffraction, the phenomenon whereby light waves bend around obstacles or edges. As a laser beam traverses through space, diffraction gradually causes it to spread out, ultimately leading to divergence. The Rayleigh Range signifies the domain within which the beam’s width approximately doubles from its initial dimensions, while its intensity distribution conforms to a Gaussian curve.
In this article I would like to talk a little bit more about the concept of laser Rayleigh Range. In order to start the explanation, please see, in figure 1, an hypothetical Gaussian Beam after being focused by a lens.
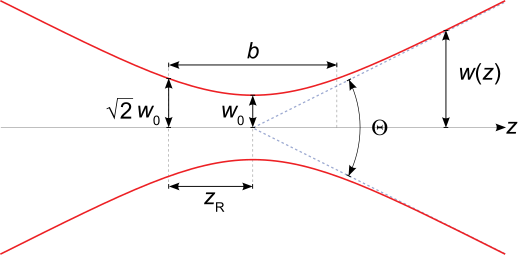
Figure 1. Gaussian beam traveling in free-space. The beam waist (w0) is the smallest diameter of the beam. Zr is the Rayleigh Range, b is the confocal distance, and ? is the divergence.
In order to explain the laser Rayleigh range we need to understand the concept of beam waist. Even though we may imagine that light from a laser is perfectly collimated and doesn’t change dimensions, the truth is that it will have some divergence, meaning that the diameter of the beam will increase as it propagates in space. There will be one point in which the beam diameter will be the smallest, that’s what we called the beam waist (w0) and we usually use it as an origin to start measuring the z-direction. So by definition, the origin (z=0) is located at the beam waist.
From there we can define the Rayleigh Range as the distance from the beam waist where the area of the Gaussian beam doubles, or in other words, where the diameter of the beam increases by sqrt(2) times the beam waist. This can be expressed in a formula as:
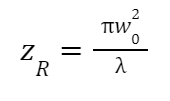
Where λ is the wavelength.
Twice the Rayleigh Range is called the confocal distance or more commonly known as the depth-of-focus. Which can be understood as a tolerance of where the image plane can be placed without a lot of image degradation. If any of you is familiar with photography, the depth-of-focus is where the image will appear to be in focus on the camera sensor.
Another reason why the Rayleigh range is important is that within this range the divergence of the beam is very small. So if you are in need to work with a highly collimated beam, your best chance is to work with a beam with a large Rayleigh Range.
In terms of field of curvature, within the Rayleigh range we can consider that the Gaussian Beam has a plane wavefront (with a Gaussian Intensity distribution), while beyond the Rayleigh range the wavefront can be considered spherical. That change in wavefront can help us to simplify or to better model our optical system, specially if needing to work with diffractive elements or near the diffraction limits.
Understanding the Significance of Rayleigh Range in Laser Applications
By understanding the Rayleigh Range, engineers can meticulously tailor the focusing conditions of the laser beam, ensuring optimal intensity and minimal divergence throughout the machining process. Similarly, in medical fields such as laser eye surgery, precise control over the Rayleigh Range enables surgeons to deliver focused laser beams with great accuracy, facilitating delicate procedures with enhanced efficacy and safety.
Furthermore, in the areas of telecommunications, where laser beams serve as carriers of information over extensive distances in free-space, the Rayleigh Range assumes a pivotal role. It aids in predicting signal degradation, optimizing transmission efficiency, and ultimately, ensuring seamless communication networks.
Exploring Practical Examples
To fully appreciate the impact of Rayleigh Range, let us deal into practical examples that underscore its significance in real-world scenarios. Consider the domain of laser cutting, where high-powered laser beams are employed to slice through materials with surgical precision. By strategically manipulating the Rayleigh Range, operators can ensure that the laser beam maintains optimal intensity and focus, thereby facilitating immaculate cuts across a diverse array of materials, ranging from metals to acrylics.
Furthermore, in the realm of biomedical research, laser scanning microscopy stands as a testament to the indispensable role of Rayleigh Range. By harnessing precise control over the Rayleigh Range, researchers can capture high-resolution images of biological specimens with unparalleled clarity, enabling detailed analysis and elucidation of intricate cellular structures.
Recent Advances and Future Outlook
Adaptive optics techniques are methods that dynamically adjust optical elements in real-time. This approach enhances our capability to finely tune and optimize the Rayleigh Range with great precision. By adapting the optical components to changing environmental conditions and inherent system fluctuations, adaptive optics allow laser systems to maintain optimal performance across a wide range of applications. This dynamic optimization not only ensures maximum efficiency but also opens doors to new areas of precision engineering and scientific exploration.
.
Conclusion
In conclusion, this article has explain some of the fundamental concepts of Rayleigh Range in laser technology, emphasizing its role in various applications. Practical examples have illustrated how precise control over the Rayleigh Range can lead to improved outcomes in fields ranging from laser cutting to biomedical research. Furthermore, discussions on recent advances such as adaptive optics have highlighted the continuous evolution of laser technology and its potential for future innovations. Overall, the article underscores the importance of understanding the Rayleigh Range in harnessing the full potential of lasers for diverse applications
Optimizing Light with Hot and Cold Mirrors
Learn how hot and cold mirrors are pivotal in UV and IR light control, significantly impacting optical system efficiency and performance.
Tackling Stray Light: K Correlation in Optical Design
Gain insights into managing stray light and light scattering in optical design through the lens of K Correlation. Enhance your understanding to achieve superior optical performance.
Rayleigh Range in Lasers FAQs
What is the Rayleigh Range in laser technology?
Rayleigh Range refers to the distance over which a laser beam stays focused before it starts to diverge or spread out.
How does Rayleigh Range affect laser beam quality?
It determines the beam’s focusing ability and the point at which the beam’s diameter starts to increase, impacting the overall quality of the laser output.
Can Rayleigh Range be adjusted in laser systems?
Yes, it can be adjusted by changing the beam waist or initial focusing of the laser, allowing for different applications and precision in optical systems.